SCIENCE - Malgré toutes nos connaissances, nous comprenons encore très mal le fonctionnement du cerveau. C'est en quelque sorte la machinerie biologique la plus complexe à notre portée. Depuis le début des neurosciences dans les années 60, les chercheurs ont analysé sans relâche cet organe si particulier, composé de quelque 100 milliards de neurones, qui reste bien mystérieux.
Pourtant, une équipe de chercheur affirme avoir trouvé le Saint Graal, une équation simple et élégante permettant de comprendre comment le cerveau se structure pour répondre à une stimulation. Et ce modèle serait même généralisable à toutes les espèces. Il pourrait donc, potentiellement, expliquer le fonctionnement de l'intelligence. L'affirmation semble un peu grosse et il faudra évidemment encore beaucoup, beaucoup de recherche et de travail pour la valider.
Mais ce n'est pas juste une idée en l'air. Ce système, intitulé "théorie de la connectivité", a été imaginé par une équipe de chercheurs dirigée par Joe Tsien, un chercheur reconnu internationalement, qui a publié une étude dans la revue scientifique Frontiers, le 15 novembre. Une affirmation osée et à contre-courant, mais qui s'accompagne d'un gros travail d'expérimentation. L'équation en question est on ne peut plus "simple":
![e]()
Mais que signifie cette équation? En gros, elle permet de comprendre "comment nos neurones s'assemblent et s'alignent, pas simplement pour acquérir de la connaissance et en tirer des conclusions", précise l'Université américaine d'Augusta, dans laquelle travaille Joe Tsien.
Le "N" correspond aux groupes de neurones impliqués par le cerveau et le "i" au nombre d'informations que nos méninges ont à traiter dans un domaine particulier, que l'on appelle stimuli.
Pour bien comprendre ce que signifie cette formule mathématique, il faut se rappeler comment fonctionne le cerveau. Celui-ci est constitué de milliards de neurones, qui vont réagir à des stimuli (une couleur, une forme, une odeur, etc). bref, traiter l'information qu'ils reçoivent.
En fonction de ces stimulations, certains neurones vont être activés, dans des zones bien particulières de nos méninges. "Le fait que plusieurs neurones soient activés en même temps, cela va renforcer leurs liens, donc quand on va représenter la même information, cette 'assemblée de neurones' va être réutilisée", explique au HuffPost Etienne Save, directeur de recherche au CNRS. C'est comme cela que fonctionne l'apprentissage.
Les neurones et leurs cliques
Les auteurs de l'étude parlent de "cliques" de neurones, soit un groupe de neurones qui s'active quand le cerveau doit traiter une information (par exemple, quand on lui montre du sucre). C'est le fameux "N" de l'équation "N = 2^i - 1". La nouveauté, c'est que les chercheurs affirment que le nombre de "cliques" qui sont activées dépend directement du nombre de stimulations présentées au cerveau. C'est le "i" de l'équation.
Pour simplifier, prenons une souris à qui l'on va montrer quatre types d'aliments différents. C'est le "i" de l'équation. Si on lui montre une croquette, un groupe de neurones particulier va s'activer. Si on lui montre du sucre, un autre groupe de neurones, différent, va s'activer. De même si on lui montre du riz, ou encore du lait.
Mais si on montre à la souris du sucre et du riz en même temps, c'est encore un autre groupe de neurones, différent des précédents, qui va s'activer. Pareil si on lui montre à la fois des croquettes, du lait et du sucre. Et ainsi de suite. En fait, une "clique" de neurones différente s'active pour chaque combinaison possible de ces quatre aliments.
Mathématiquement, le nombre total de combinaisons est de 2 puissance 4 (nombre d'aliments différents), soit 16, auquel il faut soustraire 1. On obtient donc 15. C'est justement "N", le nombre de groupes de neurones qui peuvent être activés au total quand l'assiette de la souris contient un, deux, trois ou quatre de ces aliments.
Donc l'équation "N = 2^i - 1" devient "15 = 2^4 - 1". Le schéma ci-dessous explicite l'équation: chaque groupe de neurones (N1 à N15) est représenté par un triangle. Chaque i, illustré par des barres de couleurs, symbolise les aliments qui sont montrés à la souris. On voit que pour chaque combinaison possible d'aliments, un groupe de neurones différent est activé. Au total, il y en a donc 15.
Si l'on refait le calcul en rajoutant du sel dans les aliments, cela donne donc 5 stimuli (i). Dans ce cas, N, le nombre de groupes de neurones, sera égal à 31, soit 2 puissance 5 moins 1.
Expériences concluantes sur des souris
Potentiellement, cette équation permettrait donc de savoir combien de groupes de neurones s'activent pour les différentes activités du cerveau. Ca, c'est pour la théorie. Mais dans leur étude, les chercheurs ont aussi testé cette formule sur plusieurs centaines de souris. Ils leurs ont donc collé des électrodes sur le cerveau pour enregistrer la réaction de milliers de neurones face à des situations données.
Par exemple, vis-à-vis de différentes nourritures, de comportements sociaux (des interactions avec d'autres souris), face au stress, etc. Les chercheurs ont ainsi enregistré sept régions différentes du cerveau et plusieurs milliers de neurones. Et les résultats collent parfaitement avec les prédictions établies à l'avance, ce qui voudrait dire que le nombre de groupes de neurones activés est bien lié au nombre de stimuli, selon la fameuse formule mathématique.
"C'est un travail expérimental de fond", précise Etienne Save. Mais le chercheur en neurosciences, qui travaille à l'université d'Aix-Marseille, est toutefois "mitigé". "Les stimulations auxquelles ont été soumis les rongeurs sont très complexes. Est-il possible que d'autres cliques réagissent au même stimuli, par exemple dans d'autres structures du cerveau?", interroge-t-il. De même, les chercheurs ayant d'abord établi leur théorie et ayant cherché à la prouver, il reste possible que des biais dans leur expérience les aient conduits à ne rien trouver d'autre... que ce qu'ils cherchaient.
![frontier]()
Le E = MC² des neurosciences ?
Les chercheurs eux-mêmes ne crient pas victoire trop vite et imaginent déjà des expériences à venir pour confirmer leurs dires. Parmi les pistes envisagées, tester cela sur des organismes plus simples, comme les larves de mouche, travailler sur des structures plus complexes du cerveau et, évidemment, voir si l'équation fonctionne bien sur le singe et l'homme.
Car c'est là l'idée de Joe Tsien, pour qui "cette logique mathématique simple peut expliquer les calculs effectués par le cerveau à travers tout le spectre évolutif, allant des réseaux neuronaux les plus simples aux plus complexes". En clair, "il estime que c'est un principe indépendant de l'évolution, qui se retrouvera quelle que soit l'espèce", détaille Etienne Save.
Les auteurs concluent en se demandant si cette théorie ne pourrait pas avoir, à terme, des applications dans le domaine de l'intelligence artificielle. Pour l'instant, on est loin d'une quelconque application et ce travail reste purement fondamental et théorique. Mais "une théorie unificatrice du cerveau, c'est ce que tout le monde cherche, ce serait un progrès majeur", précise Etienne Save, qui n'y croit pour autant pas trop pour le moment.
Mais c'est après tout le fonctionnement même de la recherche scientifique: élaborer des théories, les tester, se tromper souvent, pour parfois permettre de faire des bonds de géants. Et si cette équation fonctionne vraiment, ce pourrait bien devenir le E = MC² des neurosciences.
Pourtant, une équipe de chercheur affirme avoir trouvé le Saint Graal, une équation simple et élégante permettant de comprendre comment le cerveau se structure pour répondre à une stimulation. Et ce modèle serait même généralisable à toutes les espèces. Il pourrait donc, potentiellement, expliquer le fonctionnement de l'intelligence. L'affirmation semble un peu grosse et il faudra évidemment encore beaucoup, beaucoup de recherche et de travail pour la valider.
Mais ce n'est pas juste une idée en l'air. Ce système, intitulé "théorie de la connectivité", a été imaginé par une équipe de chercheurs dirigée par Joe Tsien, un chercheur reconnu internationalement, qui a publié une étude dans la revue scientifique Frontiers, le 15 novembre. Une affirmation osée et à contre-courant, mais qui s'accompagne d'un gros travail d'expérimentation. L'équation en question est on ne peut plus "simple":
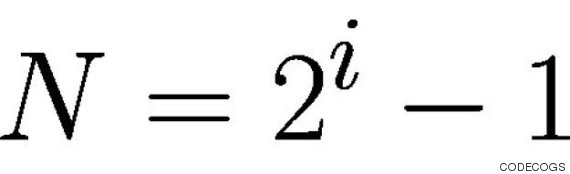
Mais que signifie cette équation? En gros, elle permet de comprendre "comment nos neurones s'assemblent et s'alignent, pas simplement pour acquérir de la connaissance et en tirer des conclusions", précise l'Université américaine d'Augusta, dans laquelle travaille Joe Tsien.
Le "N" correspond aux groupes de neurones impliqués par le cerveau et le "i" au nombre d'informations que nos méninges ont à traiter dans un domaine particulier, que l'on appelle stimuli.
Pour bien comprendre ce que signifie cette formule mathématique, il faut se rappeler comment fonctionne le cerveau. Celui-ci est constitué de milliards de neurones, qui vont réagir à des stimuli (une couleur, une forme, une odeur, etc). bref, traiter l'information qu'ils reçoivent.
En fonction de ces stimulations, certains neurones vont être activés, dans des zones bien particulières de nos méninges. "Le fait que plusieurs neurones soient activés en même temps, cela va renforcer leurs liens, donc quand on va représenter la même information, cette 'assemblée de neurones' va être réutilisée", explique au HuffPost Etienne Save, directeur de recherche au CNRS. C'est comme cela que fonctionne l'apprentissage.
Les neurones et leurs cliques
Les auteurs de l'étude parlent de "cliques" de neurones, soit un groupe de neurones qui s'active quand le cerveau doit traiter une information (par exemple, quand on lui montre du sucre). C'est le fameux "N" de l'équation "N = 2^i - 1". La nouveauté, c'est que les chercheurs affirment que le nombre de "cliques" qui sont activées dépend directement du nombre de stimulations présentées au cerveau. C'est le "i" de l'équation.
Pour simplifier, prenons une souris à qui l'on va montrer quatre types d'aliments différents. C'est le "i" de l'équation. Si on lui montre une croquette, un groupe de neurones particulier va s'activer. Si on lui montre du sucre, un autre groupe de neurones, différent, va s'activer. De même si on lui montre du riz, ou encore du lait.
Mais si on montre à la souris du sucre et du riz en même temps, c'est encore un autre groupe de neurones, différent des précédents, qui va s'activer. Pareil si on lui montre à la fois des croquettes, du lait et du sucre. Et ainsi de suite. En fait, une "clique" de neurones différente s'active pour chaque combinaison possible de ces quatre aliments.
Mathématiquement, le nombre total de combinaisons est de 2 puissance 4 (nombre d'aliments différents), soit 16, auquel il faut soustraire 1. On obtient donc 15. C'est justement "N", le nombre de groupes de neurones qui peuvent être activés au total quand l'assiette de la souris contient un, deux, trois ou quatre de ces aliments.
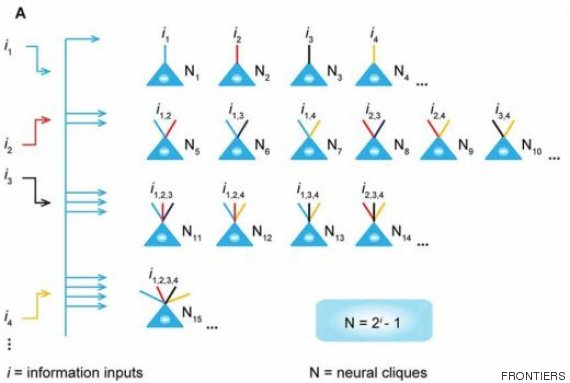
Donc l'équation "N = 2^i - 1" devient "15 = 2^4 - 1". Le schéma ci-dessous explicite l'équation: chaque groupe de neurones (N1 à N15) est représenté par un triangle. Chaque i, illustré par des barres de couleurs, symbolise les aliments qui sont montrés à la souris. On voit que pour chaque combinaison possible d'aliments, un groupe de neurones différent est activé. Au total, il y en a donc 15.
Si l'on refait le calcul en rajoutant du sel dans les aliments, cela donne donc 5 stimuli (i). Dans ce cas, N, le nombre de groupes de neurones, sera égal à 31, soit 2 puissance 5 moins 1.
Expériences concluantes sur des souris
Potentiellement, cette équation permettrait donc de savoir combien de groupes de neurones s'activent pour les différentes activités du cerveau. Ca, c'est pour la théorie. Mais dans leur étude, les chercheurs ont aussi testé cette formule sur plusieurs centaines de souris. Ils leurs ont donc collé des électrodes sur le cerveau pour enregistrer la réaction de milliers de neurones face à des situations données.
Par exemple, vis-à-vis de différentes nourritures, de comportements sociaux (des interactions avec d'autres souris), face au stress, etc. Les chercheurs ont ainsi enregistré sept régions différentes du cerveau et plusieurs milliers de neurones. Et les résultats collent parfaitement avec les prédictions établies à l'avance, ce qui voudrait dire que le nombre de groupes de neurones activés est bien lié au nombre de stimuli, selon la fameuse formule mathématique.
"C'est un travail expérimental de fond", précise Etienne Save. Mais le chercheur en neurosciences, qui travaille à l'université d'Aix-Marseille, est toutefois "mitigé". "Les stimulations auxquelles ont été soumis les rongeurs sont très complexes. Est-il possible que d'autres cliques réagissent au même stimuli, par exemple dans d'autres structures du cerveau?", interroge-t-il. De même, les chercheurs ayant d'abord établi leur théorie et ayant cherché à la prouver, il reste possible que des biais dans leur expérience les aient conduits à ne rien trouver d'autre... que ce qu'ils cherchaient.
Le E = MC² des neurosciences ?
Les chercheurs eux-mêmes ne crient pas victoire trop vite et imaginent déjà des expériences à venir pour confirmer leurs dires. Parmi les pistes envisagées, tester cela sur des organismes plus simples, comme les larves de mouche, travailler sur des structures plus complexes du cerveau et, évidemment, voir si l'équation fonctionne bien sur le singe et l'homme.
Car c'est là l'idée de Joe Tsien, pour qui "cette logique mathématique simple peut expliquer les calculs effectués par le cerveau à travers tout le spectre évolutif, allant des réseaux neuronaux les plus simples aux plus complexes". En clair, "il estime que c'est un principe indépendant de l'évolution, qui se retrouvera quelle que soit l'espèce", détaille Etienne Save.
Les auteurs concluent en se demandant si cette théorie ne pourrait pas avoir, à terme, des applications dans le domaine de l'intelligence artificielle. Pour l'instant, on est loin d'une quelconque application et ce travail reste purement fondamental et théorique. Mais "une théorie unificatrice du cerveau, c'est ce que tout le monde cherche, ce serait un progrès majeur", précise Etienne Save, qui n'y croit pour autant pas trop pour le moment.
Mais c'est après tout le fonctionnement même de la recherche scientifique: élaborer des théories, les tester, se tromper souvent, pour parfois permettre de faire des bonds de géants. Et si cette équation fonctionne vraiment, ce pourrait bien devenir le E = MC² des neurosciences.
Retrouvez les articles du HuffPost Tunisie sur notre page Facebook.